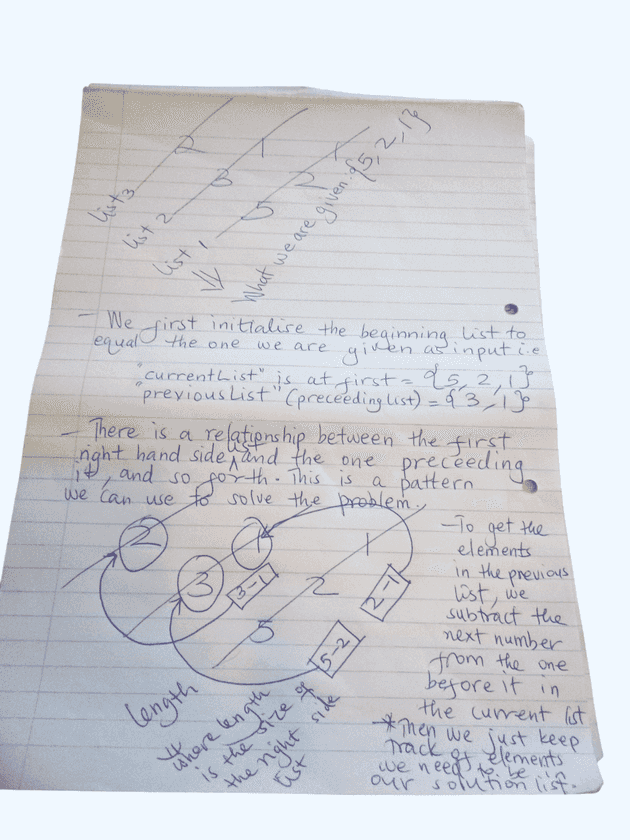
Introduction
Have you ever encountered a mathematical puzzle that makes you think backwards? Today, we'll explore an interesting challenge called "Upside-Down Pyramid Addition" and learn how to reverse engineer its original numbers.
What is Upside-Down Pyramid Addition?
Upside-Down Pyramid Addition is a process where you take a list of numbers and add adjacent pairs until you're left with a single number. For example:
2 1 1
3 2
5The numbers 2, 1, 1 form the base, and each row above is created by adding adjacent numbers until we reach the top number 5.
The Challenge
The interesting twist in this challenge is that we're given the right side of the pyramid (5, 2, 1) and need to find the original numbers [2, 1, 1]. It's like having the answer and working backwards to find the question!
Solution
import java.util.Arrays;
class Main {
public static void main(String[] args) {
int[] rightSideList = {2, 1};
System.out.println("{2, 1} =>" + Arrays.toString(upsideDownPyramidAddition(rightSideList)));
}
public static int[] upsideDownPyramidAddition(int[] array) {
int length = array.length;
int[] resultList = new int[length];
resultList[length - 1] = array[length - 1];
int previousLength = length - 1;
int[] currentList = Arrays.copyOf(array, length);
for (int i = 0; i < length - 1; i++) {
int[] previousList = new int[previousLength];
for (int j = 0; j < previousLength; j++) {
previousList[j] = currentList[j] - currentList[j + 1];
}
resultList[previousLength - 1] = previousList[previousLength - 1];
previousLength--;
currentList = previousList;
}
return resultList;
}
}Breaking Down the Solution
Let's analyze how our Java solution works:
- Setup Phase
int[] resultList = new int[length];
resultList[length - 1] = array[length - 1];We know the last number in our result will be the same as the last number in our input, so we start there.
- Working Backwards
for (int i = 0; i < length - 1; i++) {
int[] previousList = new int[previousLength];
for (int j = 0; j < previousLength; j++) {
previousList[j] = currentList[j] - currentList[j + 1];
}
}The key insight is that each number in the original list can be found by subtracting consecutive numbers in the right side of the pyramid.
Example Walkthrough
Let's say we have [5, 2, 1]:
- Start with last number: 1
- Work backwards: 2 - 1 = 1
- Continue: 5 - 2 = 3
- Result: [2, 1, 1]
Key Insights
- The process is deterministic - there's only one possible original list for each right side
- We can use subtraction to reverse the addition process
- The algorithm works from bottom to top, right to left
Time Complexity
Let's analyze the time complexity of the Upside-Down Pyramid Addition algorithm:
public static int[] upsideDownPyramidAddition(int[] array) {
int length = array.length; // O(1)
int[] resultList = new int[length]; // O(1)
resultList[length - 1] = array[length - 1]; // O(1)
int previousLength = length - 1; // O(1)
int[] currentList = Arrays.copyOf(array, length); // O(n)
// Outer loop runs (length-1) times
for (int i = 0; i < length - 1; i++) { // O(n)
int[] previousList = new int[previousLength]; // O(1)
// Inner loop runs (previousLength) times
// previousLength decreases by 1 in each iteration
for (int j = 0; j < previousLength; j++) { // O(n-1), O(n-2), ... O(1)
previousList[j] = currentList[j] - currentList[j + 1];
}
resultList[previousLength - 1] = previousList[previousLength - 1];
previousLength--;
currentList = previousList;
}
return resultList;
}Let's break down the nested loops:
- The outer loop runs (n-1) times where n is the length of the input array
- The inner loop runs:
- (n-1) times in first iteration
- (n-2) times in second iteration
- (n-3) times in third iteration
- And so on...
This forms an arithmetic sequence: (n-1) + (n-2) + (n-3) + ... + 1
The sum of this arithmetic sequence is:
(n-1)(n-1+1)/2 = n(n-1)/2Therefore:
- Time Complexity: O(n²)
- Space Complexity: O(n) - we use additional arrays of decreasing size
Here's a visual representation for input [5,2,1]:
Iteration 1: [5,2,1] → need to process 2 numbers
Iteration 2: [3,1] → need to process 1 number
Final: [2,1,1]
Total operations = 2 + 1 = 3For a larger input [10,6,3,2]:
Iteration 1: [10,6,3,2] → process 3 numbers
Iteration 2: [4,3,1] → process 2 numbers
Iteration 3: [1,2] → process 1 number
Final: [3,1,2,2]
Total operations = 3 + 2 + 1 = 6The quadratic time complexity means this algorithm might not scale well for very large inputs, but it's efficient enough for the typical use case where the pyramid height is relatively small.
Optimized Algorithm
We can improve the algorithm in a few ways. Here's an optimized version with explanations:
class Solution {
// Optimized solution: O(n) time complexity
public static int[] upsideDownPyramidAddition(int[] rightSide) {
int n = rightSide.length;
int[] result = new int[n];
// Last number is always the same
result[n-1] = rightSide[n-1];
// Calculate each original number in one pass
for (int i = n-2; i >= 0; i--) {
result[i] = rightSide[i] - result[i+1];
}
return result;
}
}Key Improvements:
-
Time Complexity: Reduced from O(n²) to O(n)
- Single pass through the array instead of nested loops
- Each element is processed exactly once
-
Space Complexity: Reduced from O(n) to O(1) extra space
- Only one result array needed instead of multiple temporary arrays
- No need for copying arrays
-
Code Simplicity:
- Reduced from ~20 lines to ~10 lines
- More readable and maintainable
- Less prone to bugs
Let's understand how it works:
Given right side: [5,2,1]
Step 1: Initialize result array
result = [0,0,1] // Last number is same as input
Step 2: Work backwards
i = 1: result[1] = rightSide[1] - result[2]
result[1] = 2 - 1 = 1
result = [0,1,1]
i = 0: result[0] = rightSide[0] - result[1]
result[0] = 5 - 3 = 2
result = [2,1,1]The mathematical insight that enables this optimization:
- In the pyramid, each number is the sum of two numbers below it
- Therefore, each original number can be found by subtracting the next number in our result from the corresponding number in the right side
Visual proof:
Original: 2 1 1
\ /\ /
Result: 3 2
\ /
[5]
If we know 5 and 2:
- To get the first number (2): 5 - 2 = 3
- To get the second number (1): 2 - 1 = 1This solution is:
- More efficient
- More scalable
- Easier to understand and maintain
- Less memory intensive
Conclusion
This challenge demonstrates how mathematical patterns can be reversed using systematic thinking. By understanding the original process, we can work backwards to find our solution.
Practice Challenge
Try implementing this solution in your preferred programming language. Can you optimize it further? Can you handle edge cases like single-element arrays?
Remember: Sometimes the best way to solve a problem is to understand how it was created in the first place!